Proceedings of the 2nd Workshop on Adaptive Systems and User Modeling on the WWW

Adaptivity in the KBS Hyperbook System

Nicola Henze and Wolfgang Nejdl
Knowledge Based Systems Group
University of Hannover, Lange Laube 3, 30159 Hannover, Germany
Phone: +49 511 762 9711, Fax: +49 511 762 9712
e-mail: {henze | nejdl}@kbs.uni-hannover.de

Abstract: We have implemented an adaptive hyperbook system (KBS Hyperbook) for an introductory course on computer science (CS1). The adaptation techniques used for this course are based on a goal-driven approach. This allows students to choose their own learning goals and to get suggestions for suitable projects and information units covering the knowledge required to reach these learning goals. In addition, sequential paths through the hyperbook are generated which provide the student with required knowledge. The student modeling component underlying our hyperbook system uses a model of the application domain which contains knowledge items (KI) covered by the particular hyperbook and learning dependencies between these KIs. For calculating the system's belief of a user's knowledge on each KI we use a Bayesian network. We propose a project selection algorithm based on user goals and previous knowledge, and a constructive trail mechanism that generates guided tours through the hyperbook containing all prerequisites needed by a particular user to perform a specific project.

Keywords: Educational Hypermedia, Adaptive Hypermedia on the WWW

Introduction

One of the main goals of student modeling in educational hypermedia is student guidance [2]. Students have learning goals and previous knowledge which should be reflected by the hyperbook for adapting the content or the link structure of the hyper document. For our KBS hyperbook system we follow a constructivistic pedagogic approach, building on project based learning, group work and discussions [10]. Such a project-based learning environment leads to new requirements for adaptation, in order to adapt the project resources presented in a set of hypermedia documents to the student's goals for a specific project and the student's knowledge. It has to support the student learner by implementing the following adaptation functionality:

$\bullet$

Adaptive Information Resources: give the students appropriate information while performing their projects, by annotating necessary project resources depending on current student's knowledge

$\bullet$

Adaptive Navigational Structure: adapt/annotate the navigational structure in order to give the student additional information about appropriate material to explore/learn next

$\bullet$

Adaptive Trail Generation: provide guidance by generating a sequential trail through parts of the hyperbook, depending on a student's goals

$\bullet$

Adaptive Project Selection: provide suitable projects depending on student goals and previous knowledge

$\bullet$

Adaptive Goal Selection: propose suitable learning goals depending on the particular user's knowledge

In this paper we will describe the implementation of these adaptation requirements within our hyperbooks.

The hyperbook model

Figure 1 shows part of the high level structure of our hyperbook, and, simultaneously, the different learning strategies in our environment, and the resulting link adaptation tasks. The notation we use in this figure is a kind of ER-modeling notation which shows concepts as boxes, relations (1:1, 1:n, m:n) as links, and two kinds of adapted relations. The main content of the hyperbook consists of semantic information units and project units. Both of these refer to the actual content to be displayed on the WWW as pages of the hyperbook (see [8,9] for a description of the basic principles and the implementation of the KBS hyperbook system).

Figure 1: Part of the meta model for hyperbooks

All implemented adaption strategies in our hyperbook are based on knowledge items. Such a knowledge item ( $KI$) denotes a knowledge concept of the application domain. These concepts could be elementary, for example the "if"- or "while"-concepts in a programming language, or compound, like "knowledge about flow control statements". All $KI$s are connected in a single dependency graph as described in section 1.1.3. The knowledge items are used for indexing the contents of information units, project units and for describing the range of goals. They are similar to the domain model concepts used in [3].

Information units do not correspond to syntactical parts of a book (such as sections or chapters), but semantical parts (such as information units about "java objects", "iteration constructs", "parameters", etc.). They are semantically related to other information units (i.e. "object" and "object instantiation" are related information units). These semantic relationships generate the navigational structure between the information units (which is done dynamically by the KBS hyperbook system), so each link between information units corresponds to some kind of semantic relationship between these units. For discussion of these semantic relationships we refer to [15]. This navigational structure can be annotated as "already known", "suggested", "too difficult", according to the current knowledge of the reader ( adaptive navigational structure). For this annotation, we use the well known traffic light metaphor (see e.g. [3,19]).

Information units are indexed by knowledge items. As information units are already semantic entities, in many cases we have a one to one correspondence between information units and knowledge items. One or more of the knowledge items belonging to a page are the main knowledge items, and for each knowledge item there is exactly one information unit, where it is a main knowledge item (see figure 2).

Figure 2: Measuring contents of Hyperbook-pages

So we have something like a knowledge item index, which gives for each knowledge item one main information unit, and some other information units where it occurs, too, but not as main knowledge item.

Project units contain project description, e.g. excercises or examples of solved problems. We call them projects because we want to emphasize that these excercises are designed like real-world problems (see constructivist learning theory), embedded in a complex context. Consider for example the project "security concepts in Java". Here the task for the students is to write a secure Java programm which saves some data in a file on the network. The situation in which this programm should work is described, as well as some hints: What should happen if the network is not reachable? What to do if the permissions of the file are not correct? etc. To support the student's work on the project the system has to compute relevant semantic information units.

The project units are indexed by those knowledge items which the student needs to know in order to work successfully on these projects. The relationship between project units and information units can be derived automatically via the knowledge items and shows the information units which are relevant for a given project. The links corresponding to this relationship can be adapted as well. This is done by annotating the links according to the user's knowledge ("already known", "suggested", "too difficult"), leading to an adaptive information resource for a given project. The annotated links are shown as an annotated index (from the project unit to the corresponding information units). The above mentioned project "security concepts in Java" can be successfully solved by using different solution strategies: E.g. the student could use Java's predefined exceptions or user-defined exceptions, the exceptions can be grouped for effective error handling, etc. Thus this project should be indexed by the $KI$s about error handling, grouping of exception, etc. Since the $KI$s are connected in a dependecy graph it is sufficient to index this project with only one $KI$, which aggregates knowledge about exception handling in Java.

The system can also generate a sequential trail (guided tour) through these information units relevant for a project, leaving out already known information units, and ordering the remaining information units, such that difficult information units are suggested at a later stage, when the user knows enough in order to understand them ( adaptive trail generation). For the project "security concepts in Java", the generated trail is the sequence of the semantic information units "exception in Java", "What are security exceptions?", "input / output exceptions", "grouping of exceptions", "handling exceptions" and "exception hierarchy". The example project and the trail can be seen in figure 3.

Figure 3: Example page of the Hyperbook with a computed trail applet.
The hyperbook on CS1 is available at http://www.kbs.uni-hannover.de/hyperbook/

The user can select a set of knowledge items called a goal, and the system can generate an index of projects most useful for achieving the user's learning goal ( adaptive project selection), a trail for learning these knowledge items adapted to the user's knowledge, or an annotated index of information units for this goal. Finally, the hyperbook system can propose suitable learning goals based on the user's current knowledge ( adaptive goal selection), and then propose corresponding projects, trails, or information units.

The student model

The student modeling component used in the KBS hyperbook system is based on a pedagogical model of the domain of a hyperbook. This pedagogical model contains the knowledge items mentioned in the previous section and adds a partial order between these $KI$s to represent learning dependencies, where KI₁ < KI₂ denotes the fact that KI₁ has to be learned before KI₂, because understanding KI₁ is a prerequisite for understanding KI₂.

The student model also contains descriptions of each user's current knowledge in the form of a $KI$-vector. This $KI$-vector contains for every $KI$ the system's estimation about a particular student's knowledge. Observations about the student's work with the hyperbook are stored in terms of a $KI$: Each observation expresses the grade of knowledge the user has on a $KI$. We use four grades: A student can have "expert's knowledge" on a $KI$, "advanced knowledge", "beginner's knowledge" or "newcomer's knowledge". Since we represent the user's knowledge on a $KI$ as a probability distribution, finer grades are possible as well.

The separation of hyperbook model and pedagogical model has advantages for authoring the hyperbook, as learning dependencies between knowledge items are described once in the pedagogical model, and the dependencies between information units of the hyperbook can be inferred automatically from the $KI$ -dependencies and the indexing of the information units by the $KI$s. The implementation technique used in our student model component is a Bayesian network¹. This BN contains the knowledge items as network nodes. The dependencies between $KI$s are expressed by conditional probabilities between the $KI$s (a detailed description can be found in a technical report [11]). The observations about a user encoded in the grades of knowledge the user has about a $KI$ are directly used as input for the BN. BNs are very useful for our student modeling approach, since they allow to describe the application domain in a single dependency graph which contains all necessary prerequisites for a particular knowledge item and models dependencies among knowledge items. By using a Bayesian network we are able to infer, for example, that a user mastering an advanced topic has also knowledge about the required prerequisites of this topic.

Observing the User

There are several systems which use the fact, that the user "reads" some information, to update the estimate of the user's knowledge (e.g. [3]), and also include reading time and/or the sequence of read pages to enhance this estimation. While this is a viable approach, it has the disadvantage, that it is difficult to measure the knowledge a user gains who "reads" a HTML-page [2]. In the current state of our development, we decided neither to take information about visited pages into account nor the user's path through the hypertext. Instead we use only the projects for updating the system. Either we ask the student for direct feedback after working on a project: The student judges her/his performance in the categories "topic was easy - I mastered it effortless", "topic was okay - but some problems were arising", "topic was hard - I had a few ideas but could not get the thing right" and "no idea about this topic at all". Or we ask some experts to judge the student's project performance and use this judgement as observations about the student's work.

Adaptive Information Resources and Trail Generation

Often a user needs information about specific topics but lacks prerequisite knowledge for these topics (e.g. a user wants to work on a project about "algorithms" but does not understand "simple control structures" or "methods"). In such circumstances it does not help to start reading the information unit about "algorithms". To support the user in this situation, we compare the user's actual knowledge with the required knowledge needed to understand the requested topic. If the user lacks some requirements we generate a sequence of information units (trail or guided tour) that guides his learning towards the selected topic.

Generating such a trail is implemented by a depth-first-traversal algorithm which checks the system's estimate of the user's knowledge of those $KI$s that are prerequisites for the actual goal. The algorithm checks if all prerequisite knowledge is sufficiently known by the user; if not, the corresponding information units of the hyperbook are marked. Afterwards a sequence of all those marked units is generated which leads from the simple to the complicated topics unto the selected topic. Furthermore, the hyperbook provides direct access to information resources needed for the actual task (information goal or project). This information resource is generated by the same depth-first-traversal algorithm as mentioned above but contains all found informations units. It is displayed as a sorted index, each link annotated according to the user's knowledge by using the traffic light metaphor.

Adaptive Project Selection

In order to select suitable projects for a user the hyperbook contains a project library. Each project is indexed by the $KI$s that have to be understood in order to successfully complete the project. These $KI$s are weighted due to their relevance for the project. As we use a Bayesian network for modeling the user's knowledge, we do not have to include prerequisite knowledge items, because they are already taken care of by the dependency structure modelled in the BN. For example, the project "security concepts in Java" mentioned above is indexed by the $KI$ "exception handling" with a relevance of 100%; a project "thinking about cars" which is an introduction to the ideas of objects, is indexed by the $KI$s "classes in object-orientation" (30%), "objects" (20%), "messages" (20%), and "inheritance" (30%). The fact that the relevancies sum up to 100% is only a matter of computation. We plan to provide forms for the authors of projects where they could determine the relevance of a $KI$ for a project by using sliders.

A project is useful for a user in his current knowledge state and his situation, if

$\bullet$

the $KI$s comprising the user's goal are sufficiently contained in this project, and

$\bullet$

all $KI$s which are not part of the user's goal but necessary for the project, are understood well.

These requirements determine the selection criteria for finding an appropriate project for a user that helps the user to achieve his or her learning goal and reflects his or her current knowledge state. They are implemented by two algorithms. The first one calculates how good a project matches the goal of a user ( project-goal-distance). The second one determines whether the actual knowledge of a user is sufficient for performing the suggested project without too many difficulties ( fitness). For example, a student who is interested in learning simple control structures in Java will have difficulties with a project that uses control structures to build a graphical user interface if she/he has only "beginner's knowledge" about graphical user interfaces.

The hyperbook selects the best project(s) by comparing the weighted sums of these two measures. The weights allow to emphasize either one of the aspects matching and fitness. Currently, we emphasize matching. This will change if more projects with overlapping content are added to the hyperbook. For example, if we have four projects concerned with exception handling in Java, fitness will become more relevant to determine the project that introduces the relevant goal concepts tailored to the user's current knowledge state.

Matching of Projects and Goals

We implemented a matching algorithm that calculates the project-goal-distance between a project and the actual goal based on the $KI$s contained in the goal and their relevance in the project. Each $KI$ contained in the goal is assumed to have a relevance of 100%. The relevance of a $KI$ for a project is defined by its percentage in relation to the whole project. The matching algorithm uses the euclidean metric to calculate the distance between a $KI$ that belongs to the user's goal and its relevance for the project. A short distance means that this $KI$ is very important for performing the project while a large value represents the fact that the $KI$ is not very relevant for the project. For every $KI$ of the goal that is not contained in the project, this distance is set to a maximum value of 100. Thus,

$$\begin{eqnarray*}\forall KI \in \mbox{goal}: \qquad\mbox{distance} \left(KI,......n P$} \\100& \mbox{, other cases} \\\end{array} \right.\end{eqnarray*}$$

To make projects indexed by different numbers of $KI$s comparable, the project-goal-distance for a project and a given goal is calculated as the mean value of all these distances:

$$\nonumber\mbox{project-goal-distance(Goal } G,\mbox{ Projec......} \mbox{distance}(KI, P) }{\displaystyle \sum_{KI \in G} 1}$$

Fitness

The second algorithm determines the fitness of a user for a project. To determine this fitness we evaluate the knowledge of the user concerning those parts of the project that do not belong to the user's goal. This enables us to select projects that are based on prerequisites already known by the user, and thus lead him as fast as possible to his goal.

$$\nonumber\mbox{fitness} = \frac{ \displaystyle \sum_{i=1}^n......\sum_{i=1}^n ID \left( KI_i \notin \mbox{goal}\right)}\quad$$

where KI₁, .. , KI_n index the project and ID is the identity function that returns 1, if KI_i is not contained in the goal, 0 otherwise. Knowledge(KI_i) is the system's belief that the user knows KI_i.

Adaptive Goal Selection

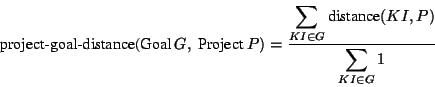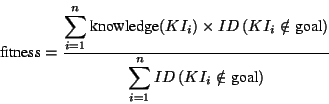If a user wants more guidance during his learning he may ask the hyperbook for the next learning step. This request is resolved by determining a suitable learning goal depending on his current knowledge. Based on this goal, the hyperbook can propose a suitable project, a set of information units or a trail leading to that goal. To determine the next suitable learning goal, a sequential trail covering the whole hyperbook is calculated. For each item of this trail the system's estimate about the user's knowledge is checked - if the user fails to know some knowledge item, this item is proposed as the next suitable goal.

Adaptive Navigational Structure

As discussed previously, the links between information units are based on their semantic relationships. Annotation of these links is very useful if a user just wants to browse through the hyperbook. Links are marked as "ready for reading" (green ball in front of a link), "not ready for reading" (red ball) or "already known" (grey ball) to help the user select appropriate information units.

Related Work

In this section we will specifically compare our system to other hyperbook-like approaches and to other systems which use similar techniques for indexing and describing relevant information, and to systems that use Bayesian networks for maintaining a user's knowledge. ELM-ART [19] and its successors implement episodic user modeling based on a hierarchically organized conceptual network for knowledge representation. Each unit of the network contains the text of the page, information to relate this page to other units, and a description about incoming, outgoing, and related concepts. Thus the conceptual network contains both information about the application domain and the reading sequence. We use two different models for describing the user and the application domain. Therefore the author does not need to model incoming and outcoming pages explicitly, but store dependency information in a separate user model (the Bayesian network). Observations about the learning progress of a particular user can be used to update the user model independently from particular page. The system is able to infer for example that prerequisite knowledge of a $KI$ has already been acquired by a user if the knowledge item itself is understood by the user. The way ELM-ART uses learning units is very different to our system as we generate individualized learning units for the users.

The technique of indexing every page with concepts learned by reading a page, prerequisite knowledge and, in addition, the prerequisite that makes this page superfluous, is also used by [5]. The authoring tool provided in Interbook [4,3], which evolved from the ELM-ART tutoring system, uses a hierarchically organized domain model based on texts structured with sections, subsections, etc. Based on this domain model, pages of the electronic textbook are generated. Pop [12] uses a hierarchy for knowledge representation. These approaches of using an explicit domain model are similar to our approach, but we allow generally structured domain models based (e.g. based on the description of a software engineering process ("process", "phases", "activities")). PT [14] uses three levels for a customized hypertext: A domain representation level, stereotypes and an individual model. A meta hypertext is used to cover examples of different sorts (mathematical, text-based, tiny-focussed, larger-complete) thus this meta model has a different role as the meta model used in our hyperbooks as it handles pages with different attributes. The used implementation technique (e.g. preprocessor commands) is very different from our approach and handles page adaption. The use of knowledge components for structuring the domain is very similar to the way we model the conditional dependencies for our BN: more general concepts are splitted into refined concepts which themselves may be splitted into refined concepts, etc.

A comprehensive review of current work in using uncertainty management techniques in user modeling is given in [13]. Systems using Bayesian networks are for example [1,6] that employ BNs for plan recognition and coached problem solving. EPI-UMOD [17] uses separate BNs for each of a number of concrete user categories in which special conditional dependencies between knowledge items for each stereotype are implemented. POKS [7] constructs a network of implication relations among knowledge units from a small sample of user data sets. The use of BNs in our hyperbook is distinct from these approaches. We use a single, overall dependency graph for modeling the knowledge of the application domain. Clearly, this graph is not as fine grained as a graph that is suited for e.g. plan recognition as it serves different purposes. The BN used for our user model has to model dependencies among knowledge units which describe the application domain. User model and domain model are required to implement a hyperbooks. In addition, as we use a three-level model for finding dependencies among the knowledge units and a clustering mechanism for generating an acyclic graph, we implemented an exact inferring alg>rithm as proposed in [16]. Dynamic Bayesian networks are used in [18]. As we implement goal-driven learning, we have no time critical tasks (time-critical in the sense of Dynamic BNs). But we see a requirement in learning our BN out of data. This will be important as we use one overall Bayesian network for modeling the different users of our hyperbook that could be improved by learning strategies for BNs (see UAI).

Discussion and Further Work

This paper describes the adaptation functionalities of our CS1 learning environment based on active, project-based learning: adaption of information resources, adaptive navigational structures, adaptive trail generation and adaptive project and goal selection, as well as their implementation. We think that these functionalities are necessary for and enhance the utility of adaptive hypermedia systems in project oriented learning environments. The hyperbook on CS1 is available at http://www.kbs.uni-hannover.de/hyperbook/. The next step will be the evaluation of the updating functionalities made possible by the Bayesian network which stores our learning dependencies and is updated by evidences about user learning achievements with respect to our $KI$s, and the added flexibility we gained by decoupling this part of the user model from the structural and semantical units in our hyperbook. Furthermore we work on an introductory interview for determining a student's initial knowledge of the domain by asking the student to do some example project.

Bibliography

1

D. Albrecht, I. Zukerman, A. Nicholson, and A. Bud. Towards a Bayesian Model for Keyhole Plan Recognition in Large Domains. In Proceedings of the Sixth International Conference on User Modeling, UM97, Sardinia, Italy, 1997.

2

P. Brusilovsky. Methods and techniques of adaptive hypermedia. User Modeling and User Adapted Interaction, 6(2-3):87-129, 1996.

3

P. Brusilovsky and E. Schwarz. User as Student: Towards an Adaptive Interface for Advanced Web-Based Applications. In Proceedings of the Sixth International Conference on User Modeling, UM97, Sardinia, Italy, 1997.

4

P. Brusilovsky, E. Schwarz, and G. Weber. A Tool for Developing Adaptive Electronic Textbooks on WWW. In Proceedings of WebNet'96 - World Conference of the Web Society, Boston, MA, USA, June 1996.

5

L. Calvi and P. de Bra. Improving the usability of hypertext courseware through adaptive linking. In The Eighth ACM International Hypertext Conference, Southampton, UK, April 1997.

6

C. Conati, A. S. Gertner, K. VanLehn, and M. J. Druzdzel. On-Line Student Modeling for Coached Problem Solving Using Bayesian Networks. In Proceedings of the Sixth International Conference on User Modeling, UM97, Sardinia, Italy, 1997.

7

M. C. Desmarais and A. Maluf. User-Expertise Modeling with Empirically Derived Probabilistic Implication Networks. User Modeling and User Adapted Interaction, 5:283-315, 1996.

8

P. Fröhlich, N. Henze, and W. Nejdl. Meta-modeling for hypermedia design. In Proc. of Second IEEE Metadata Conference, Maryland, Sept. 1997.

9

P. Fröhlich, W. Nejdl, and M. Wolpers. KBS-Hyperbook -an Open Hyperbook System for Education. In Proceedings of the ED-MEDIA World Conference on Educational Multimedia and Hypermedia, Freiburg, Germany, June 1998.

10

N. Henze and W. Nejdl. A web-based learning environment: Applying constructivist teaching concepts in virtual learning environments. In IFIP 3.3 and 3.6 Joint Working Conference: The Virtual Campus: Trends for Higher Education and Training, Madrid, Nov. 1997.

11

N. Henze and W. Nejdl. Student Modeling for the KBS Hyperbook System using Bayesian networks. Technical report, University of Hannover, Feb. 1999. http://www.kbs.uni-hannover.de/paper/99/adaptivity.html.

12

K. Höök, J. Karlgren, A. Waern, N. Dahlbäck, C. Jansson, K. Karlgren, and B. Lemaire. A glass box approach to adaptive hypermedia. User Modeling and User Adapted Interaction, 6(2-3):157-184, 1996.

13

A. Jameson. Numerical uncertainty management in user and student modeling: An overview of systems and issues. User Modeling and User Adapted Interaction, 5, 1996.

14

J. Kay and B. Kummerfeld. User Models for Customized Hypertext. In C. Nicholas and J. Mayfield, editors, Intelligent hypertext: Advanced Techniques for the World Wide Web, LNCS Vol. 1326. Springer, 1997.

15

W. Nejdl and M. Wolpers. KBS Hyperbook - a data-driven information system on the web. Technical report, University of Hannover, Nov. 1998. http://www.kbs.uni-hannover.de/paper/99/adaptivity.html.

16

J. Pearl. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgen Kaufmann Publishers, Inc., 1988.

17

F. D. Rosis, S. Pizzutilo, A. Russo, D. C. Berry, and F. J. Molina. Modeling the User Knowledge by Belief Networks. User Modeling and User Adapted Interaction, 2:367-388, 1992.

18

R. Schäfer and T. Weyrath. Assessing Temporally Variable User Properties with Dynamic Bayesian Networks. In Proceedings of the Sixth International Conference on User Modeling, UM97, Sardinia, Italy, 1997.

19

G. Weber and M. Specht. User Modeling and Adaptive Navigation Support in WWW-Based Tutoring Systems. In Proceedings of the Sixth International Conference on User Modeling, UM97, Sardinia, Italy, 1997.

Footnotes

... network¹

A BN is defined by as set of random variables X = {X ₁, .. , X_n} with associated probabilities and a labeled directed acyclic graph G encoding conditional probabilities between these random variables. The vertices of G correspond to the random variables {X₁, .. , X_n}, and the edges represent conditional dependencies between them. A conditional dependency links a child variable to a set of parent variables, and is defined by the conditional distributions of the child variable given the configuration of its parent variables.